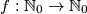
Show that there exists a bijective function such that for all :
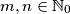
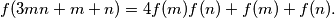
%V0
Show that there exists a bijective function $f: \mathbb{N}_{0}\to \mathbb{N}_{0}$ such that for all $m,n\in \mathbb{N}_{0}$:
$$f(3mn + m + n) = 4f(m)f(n) + f(m) + f(n).$$
Izvor: Međunarodna matematička olimpijada, shortlist 1996
Školjka 
such that for all 
: 