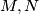
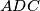
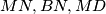
Let be a regular tetrahedron and distinct points in the planes and respectively. Show that the segments are the sides of a triangle.
%V0
Let $ABCD$ be a regular tetrahedron and $M,N$ distinct points in the planes $ABC$ and $ADC$ respectively. Show that the segments $MN,BN,MD$ are the sides of a triangle.
Izvor: Međunarodna matematička olimpijada, shortlist 1997
Školjka 
be a regular tetrahedron and 
distinct points in the planes 
and 
respectively. Show that the segments 
are the sides of a triangle.