IMO Shortlist 1997 problem 6
Dodao/la:
arhiva2. travnja 2012. (a) Let

be a positive integer. Prove that there exist distinct positive integers
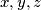
such that
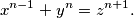
(b) Let
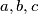
be positive integers such that

and

are relatively prime and

is relatively prime either to

or to
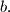
Prove that there exist infinitely many triples
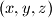
of distinct positive integers
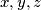
such that
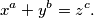
%V0
(a) Let $n$ be a positive integer. Prove that there exist distinct positive integers $x, y, z$ such that
$$x^{n-1} + y^n = z^{n+1}.$$
(b) Let $a, b, c$ be positive integers such that $a$ and $b$ are relatively prime and $c$ is relatively prime either to $a$ or to $b.$ Prove that there exist infinitely many triples $(x, y, z)$ of distinct positive integers $x, y, z$ such that
$$x^a + y^b = z^c.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1997