Školjka

• Tečajevi
• MetaMath '24
• Izbornik
• Početna
• Arhiva zadataka
• Natjecanja
• Hrvatska
• Olimpijade
• Međunarodna matematička olimpijada
• Međunarodna matematička olimpijada - Shortlist
• 2018
• 2017
• 2016
• 2015
• 2014
• 2013
• 2012
• 2011
• 2010
• 2009
• 2008
• 2007
• 2006
• 2005
• 2004
• 2003
• 2002
• 2001
• 2000
• 1999
• 1998
• 1997
• 1996
• 1995
• 1994
• 1993
• 1992
• 1991
• 1990
• 1989
• 1988
• 1987
• 1986
• 1985
• 1984
• 1983
• 1982
• 1981
• 1980
• 1979
• 1978
• 1977
• 1976
• 1975
• 1974
• 1973
• 1972
• 1971
• 1970
• 1969
• 1968
• 1967
• 1966
• 1965
• 1964
• 1963
• 1962
• 1961
• 1960
• 1959
• Srednjoeuropska matematička olimpijada
• JBMO
• ELMO
• Europski matematički kup
• Skakavac
• Mathejeva mala (m)učionica
• MNM predavanja subotom
• Simulacije
• Kamp 2013
• RADDAR
• Vekijeva Vesela Vjezbenica
• Predavanja
• Natjecanja
• Tečajevi
• 
  
• Registracija
• Prijava
• 
  
• Svi zadaci
• Rješenja
• Traži
• 
  
• 
  
• Pomoć
• O nama

IMO Shortlist 1997 problem 7

Kvaliteta:

  Avg: 0,0

Težina:

  Avg: 0,0

Dodao/la: arhiva
2. travnja 2012.

1997 geo shortlist šesterokut

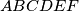
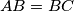
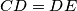
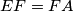
The lengths of the sides of a convex hexagon satisfy , , . Prove that:

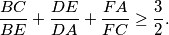
%V0 The lengths of the sides of a convex hexagon $ABCDEF$ satisfy $AB = BC$, $CD = DE$, $EF = FA$. Prove that: $$\frac {BC}{BE} + \frac {DE}{DA} + \frac {FA}{FC} \geq \frac {3}{2}.$$