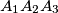
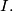
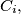
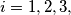
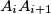
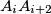
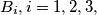
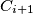
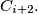
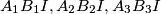
Let be a non-isosceles triangle with incenter Let be the smaller circle through tangent to and (the addition of indices being mod 3). Let be the second point of intersection of and Prove that the circumcentres of the triangles are collinear.
%V0
Let $A_1A_2A_3$ be a non-isosceles triangle with incenter $I.$ Let $C_i,$ $i = 1, 2, 3,$ be the smaller circle through $I$ tangent to $A_iA_{i+1}$ and $A_iA_{i+2}$ (the addition of indices being mod 3). Let $B_i, i = 1, 2, 3,$ be the second point of intersection of $C_{i+1}$ and $C_{i+2}.$ Prove that the circumcentres of the triangles $A_1 B_1I,A_2B_2I,A_3B_3I$ are collinear.
Izvor: Međunarodna matematička olimpijada, shortlist 1997
Školjka 
be a non-isosceles triangle with incenter 
Let 
be the smaller circle through 
tangent to 
and 
(the addition of indices being mod 3). Let 
be the second point of intersection of 
and 
Prove that the circumcentres of the triangles 
are collinear.