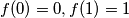
Let be a prime number and an integer polynomial of degree such that and is congruent to or modulo for every integer . Prove that .
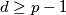
%V0
Let $p$ be a prime number and $f$ an integer polynomial of degree $d$ such that $f(0) = 0,f(1) = 1$ and $f(n)$ is congruent to $0$ or $1$ modulo $p$ for every integer $n$. Prove that $d\geq p - 1$.
Izvor: Međunarodna matematička olimpijada, shortlist 1997
Školjka 
be a prime number and 
an integer polynomial of degree 
such that 
and 
is congruent to 
or 
modulo 
. Prove that 
.