IMO Shortlist 1997 problem 13
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 In town  there are
there are  girls and
girls and  boys, and each girl knows each boy. In town
boys, and each girl knows each boy. In town  there are
there are  girls
girls 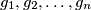 and
and 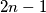 boys
boys 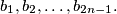 The girl
The girl 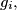
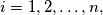 knows the boys
knows the boys 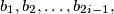 and no others. For all
and no others. For all 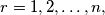 denote by
denote by 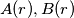 the number of different ways in which
the number of different ways in which  girls from town
girls from town  respectively town
respectively town  can dance with
can dance with  boys from their own town, forming
boys from their own town, forming  pairs, each girl with a boy she knows. Prove that
pairs, each girl with a boy she knows. Prove that 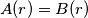 for each
for each 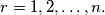
 there are
there are  girls and
girls and  boys, and each girl knows each boy. In town
boys, and each girl knows each boy. In town  there are
there are  girls
girls 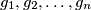 and
and 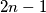 boys
boys 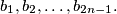 The girl
The girl 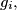
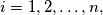 knows the boys
knows the boys 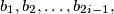 and no others. For all
and no others. For all 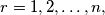 denote by
denote by 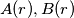 the number of different ways in which
the number of different ways in which  girls from town
girls from town  respectively town
respectively town  can dance with
can dance with  boys from their own town, forming
boys from their own town, forming  pairs, each girl with a boy she knows. Prove that
pairs, each girl with a boy she knows. Prove that 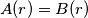 for each
for each 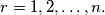
Izvor: Međunarodna matematička olimpijada, shortlist 1997
 Školjka
Školjka 
