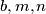
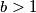
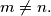
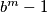
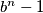
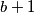
Let be positive integers such that and Prove that if and have the same prime divisors, then is a power of 2.
%V0
Let $b, m, n$ be positive integers such that $b > 1$ and $m \neq n.$ Prove that if $b^m - 1$ and $b^n - 1$ have the same prime divisors, then $b + 1$ is a power of 2.
Izvor: Međunarodna matematička olimpijada, shortlist 1997
Školjka 
be positive integers such that 
and 
Prove that if 
and 
have the same prime divisors, then 
is a power of 2.