IMO Shortlist 1997 problem 16
Dodao/la:
arhiva2. travnja 2012. In an acute-angled triangle
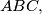
let
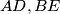
be altitudes and
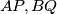
internal bisectors. Denote by

and
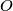
the incenter and the circumcentre of the triangle, respectively. Prove that the points
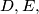
and

are collinear if and only if the points
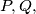
and
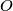
are collinear.
%V0
In an acute-angled triangle $ABC,$ let $AD,BE$ be altitudes and $AP,BQ$ internal bisectors. Denote by $I$ and $O$ the incenter and the circumcentre of the triangle, respectively. Prove that the points $D, E,$ and $I$ are collinear if and only if the points $P, Q,$ and $O$ are collinear.
Izvor: Međunarodna matematička olimpijada, shortlist 1997