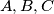
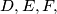
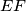
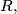
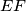
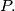
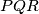
The altitudes through the vertices of an acute-angled triangle meet the opposite sides at respectively. The line through parallel to meets the lines and at and respectively. The line meets at Prove that the circumcircle of the triangle passes through the midpoint of
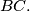
%V0
The altitudes through the vertices $A,B,C$ of an acute-angled triangle $ABC$ meet the opposite sides at $D,E, F,$ respectively. The line through $D$ parallel to $EF$ meets the lines $AC$ and $AB$ at $Q$ and $R,$ respectively. The line $EF$ meets $BC$ at $P.$ Prove that the circumcircle of the triangle $PQR$ passes through the midpoint of $BC.$
Izvor: Međunarodna matematička olimpijada, shortlist 1997
Školjka 
of an acute-angled triangle 
meet the opposite sides at 
respectively. The line through 
parallel to 
meets the lines 
and 
at 
and 
respectively. The line 
at 
Prove that the circumcircle of the triangle 
passes through the midpoint of 