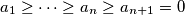
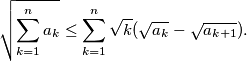
Let be real numbers. Show that Proposed by Romania
%V0
Let $a_1\geq \cdots \geq a_n \geq a_{n + 1} = 0$ be real numbers. Show that
$$\sqrt {\sum_{k = 1}^n a_k} \leq \sum_{k = 1}^n \sqrt k (\sqrt {a_k} - \sqrt {a_{k + 1}}).$$
Proposed by Romania
Izvor: Međunarodna matematička olimpijada, shortlist 1997
Školjka 
be real numbers. Show that 