IMO Shortlist 1997 problem 20
Dodao/la:
arhiva2. travnja 2012. Let

be a triangle.

is a point on the side
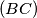
. The line

meets the circumcircle again at

.

is the foot of the perpendicular from

to

, and

is the foot of the perpendicular from

to

. Show that the line

is a tangent to the circle on diameter
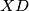
if and only if
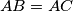
.
%V0
Let $ABC$ be a triangle. $D$ is a point on the side $(BC)$. The line $AD$ meets the circumcircle again at $X$. $P$ is the foot of the perpendicular from $X$ to $AB$, and $Q$ is the foot of the perpendicular from $X$ to $AC$. Show that the line $PQ$ is a tangent to the circle on diameter $XD$ if and only if $AB = AC$.
Izvor: Međunarodna matematička olimpijada, shortlist 1997