Let be a convex quadrilateral. The diagonals and intersect at . Show that is cyclic if and only if .
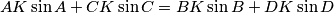
%V0
Let $ABCD$ be a convex quadrilateral. The diagonals $AC$ and $BD$ intersect at $K$. Show that $ABCD$ is cyclic if and only if $AK \sin A + CK \sin C = BK \sin B + DK \sin D$.
Izvor: Međunarodna matematička olimpijada, shortlist 1997
Školjka 
be a convex quadrilateral. The diagonals 
and 
intersect at 
. Show that 
.