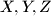
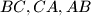
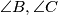
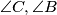
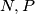
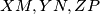
Let be the midpoints of the small arcs respectively (arcs of the circumcircle of ). is an arbitrary point on , and the parallels through to the internal bisectors of cut the external bisectors of in respectively. Show that concur.
%V0
Let $X,Y,Z$ be the midpoints of the small arcs $BC,CA,AB$ respectively (arcs of the circumcircle of $ABC$). $M$ is an arbitrary point on $BC$, and the parallels through $M$ to the internal bisectors of $\angle B,\angle C$ cut the external bisectors of $\angle C,\angle B$ in $N,P$ respectively. Show that $XM,YN,ZP$ concur.
Izvor: Međunarodna matematička olimpijada, shortlist 1997
Školjka 
be the midpoints of the small arcs 
respectively (arcs of the circumcircle of 
). 
is an arbitrary point on 
, and the parallels through 
cut the external bisectors of 
in 
respectively. Show that 
concur.