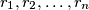
Let be real numbers greater than or equal to 1. Prove that
%V0
Let $r_{1},r_{2},\ldots ,r_{n}$ be real numbers greater than or equal to 1. Prove that
$$\frac{1}{r_{1} + 1} + \frac{1}{r_{2} + 1} + \cdots +\frac{1}{r_{n}+1} \geq \frac{n}{ \sqrt[n]{r_{1}r_{2} \cdots r_{n}}+1}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1998
Školjka 
be real numbers greater than or equal to 1. Prove that ![\frac{1}{r_{1} + 1} + \frac{1}{r_{2} + 1} + \cdots +\frac{1}{r_{n}+1} \geq \frac{n}{ \sqrt[n]{r_{1}r_{2} \cdots r_{n}}+1}.](/media/m/6/5/9/659a1db9dfb0819c970e78fed531b4ad.png)