IMO Shortlist 1998 problem C2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 Let  be an integer greater than 2. A positive integer is said to be attainable if it is 1 or can be obtained from 1 by a sequence of operations with the following properties:
be an integer greater than 2. A positive integer is said to be attainable if it is 1 or can be obtained from 1 by a sequence of operations with the following properties:
1.) The first operation is either addition or multiplication.
2.) Thereafter, additions and multiplications are used alternately.
3.) In each addition, one can choose independently whether to add 2 or
4.) In each multiplication, one can choose independently whether to multiply by 2 or by .
.
A positive integer which cannot be so obtained is said to be unattainable.
a.) Prove that if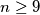 , there are infinitely many unattainable positive integers.
, there are infinitely many unattainable positive integers.
b.) Prove that if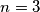 , all positive integers except 7 are attainable.
, all positive integers except 7 are attainable.
 be an integer greater than 2. A positive integer is said to be attainable if it is 1 or can be obtained from 1 by a sequence of operations with the following properties:
be an integer greater than 2. A positive integer is said to be attainable if it is 1 or can be obtained from 1 by a sequence of operations with the following properties: 1.) The first operation is either addition or multiplication.
2.) Thereafter, additions and multiplications are used alternately.
3.) In each addition, one can choose independently whether to add 2 or

4.) In each multiplication, one can choose independently whether to multiply by 2 or by
 .
. A positive integer which cannot be so obtained is said to be unattainable.
a.) Prove that if
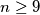 , there are infinitely many unattainable positive integers.
, there are infinitely many unattainable positive integers. b.) Prove that if
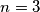 , all positive integers except 7 are attainable.
, all positive integers except 7 are attainable. Izvor: Međunarodna matematička olimpijada, shortlist 1998
 Školjka
Školjka 
