IMO Shortlist 1998 problem C3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Cards numbered 1 to 9 are arranged at random in a row. In a move, one may choose any block of consecutive cards whose numbers are in ascending or descending order, and switch the block around. For example, 9 1 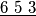
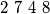 may be changed to
may be changed to 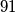
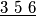
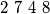 . Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
. Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
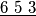
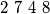 may be changed to
may be changed to 
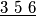
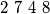 . Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
. Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order. Izvor: Međunarodna matematička olimpijada, shortlist 1998
 Školjka
Školjka 
