IMO Shortlist 1998 problem C7
Kvaliteta:
Avg: 0,0Težina:
Avg: 9,0 A solitaire game is played on an 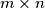 rectangular board, using
rectangular board, using  markers which are white on one side and black on the other. Initially, each square of the board contains a marker with its white side up, except for one corner square, which contains a marker with its black side up. In each move, one may take away one marker with its black side up, but must then turn over all markers which are in squares having an edge in common with the square of the removed marker. Determine all pairs
markers which are white on one side and black on the other. Initially, each square of the board contains a marker with its white side up, except for one corner square, which contains a marker with its black side up. In each move, one may take away one marker with its black side up, but must then turn over all markers which are in squares having an edge in common with the square of the removed marker. Determine all pairs 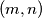 of positive integers such that all markers can be removed from the board.
of positive integers such that all markers can be removed from the board.
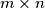 rectangular board, using
rectangular board, using  markers which are white on one side and black on the other. Initially, each square of the board contains a marker with its white side up, except for one corner square, which contains a marker with its black side up. In each move, one may take away one marker with its black side up, but must then turn over all markers which are in squares having an edge in common with the square of the removed marker. Determine all pairs
markers which are white on one side and black on the other. Initially, each square of the board contains a marker with its white side up, except for one corner square, which contains a marker with its black side up. In each move, one may take away one marker with its black side up, but must then turn over all markers which are in squares having an edge in common with the square of the removed marker. Determine all pairs 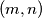 of positive integers such that all markers can be removed from the board.
of positive integers such that all markers can be removed from the board. Izvor: Međunarodna matematička olimpijada, shortlist 1998
 Školjka
Školjka 
