IMO Shortlist 1998 problem G2
Dodao/la:
arhiva2. travnja 2012. Let

be a cyclic quadrilateral. Let

and

be variable points on the sides

and

, respectively, such that
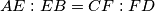
. Let

be the point on the segment

such that
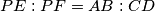
. Prove that the ratio between the areas of triangles
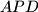
and
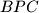
does not depend on the choice of

and

.
%V0
Let $ABCD$ be a cyclic quadrilateral. Let $E$ and $F$ be variable points on the sides $AB$ and $CD$, respectively, such that $AE:EB=CF:FD$. Let $P$ be the point on the segment $EF$ such that $PE:PF=AB:CD$. Prove that the ratio between the areas of triangles $APD$ and $BPC$ does not depend on the choice of $E$ and $F$.
Izvor: Međunarodna matematička olimpijada, shortlist 1998