IMO Shortlist 1998 problem G4
Dodao/la:
arhiva2. travnja 2012. Let

and

be two points inside triangle

such that
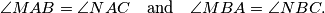
Prove that
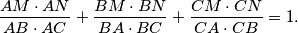
%V0
Let $M$ and $N$ be two points inside triangle $ABC$ such that
$$\angle MAB = \angle NAC\quad \mbox{and}\quad \angle MBA = \angle NBC.$$
Prove that
$$\frac {AM \cdot AN}{AB \cdot AC} + \frac {BM \cdot BN}{BA \cdot BC} + \frac {CM \cdot CN}{CA \cdot CB} = 1.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1998