IMO Shortlist 1998 problem G5
Dodao/la:
arhiva2. travnja 2012. Let

be a triangle,
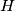
its orthocenter,
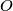
its circumcenter, and
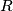
its circumradius. Let

be the reflection of the point

across the line

, let

be the reflection of the point

across the line

, and let

be the reflection of the point

across the line

. Prove that the points

,

and

are collinear if and only if
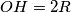
.
%V0
Let $ABC$ be a triangle, $H$ its orthocenter, $O$ its circumcenter, and $R$ its circumradius. Let $D$ be the reflection of the point $A$ across the line $BC$, let $E$ be the reflection of the point $B$ across the line $CA$, and let $F$ be the reflection of the point $C$ across the line $AB$. Prove that the points $D$, $E$ and $F$ are collinear if and only if $OH=2R$.
Izvor: Međunarodna matematička olimpijada, shortlist 1998