IMO Shortlist 1998 problem G6
Dodao/la:
arhiva2. travnja 2012. Let
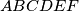
be a convex hexagon such that
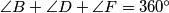
and
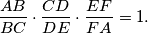
Prove that
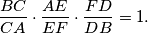
%V0
Let $ABCDEF$ be a convex hexagon such that $\angle B+\angle D+\angle F=360^{\circ }$ and $$\frac{AB}{BC} \cdot \frac{CD}{DE} \cdot \frac{EF}{FA} = 1.$$ Prove that $$\frac{BC}{CA} \cdot \frac{AE}{EF} \cdot \frac{FD}{DB} = 1.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1998