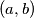
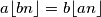
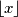
Determine all pairs of real numbers such that for all positive integers . (Note that denotes the greatest integer less than or equal to .)
%V0
Determine all pairs $(a,b)$ of real numbers such that $a \lfloor bn \rfloor =b \lfloor an \rfloor$ for all positive integers $n$. (Note that $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$.)
Izvor: Međunarodna matematička olimpijada, shortlist 1998
Školjka 
of real numbers such that 
for all positive integers 
. (Note that 
denotes the greatest integer less than or equal to 
.)