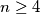
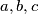
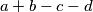
Determine the smallest integer for which one can choose four different numbers and from any distinct integers such that is divisible by .
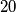
%V0
Determine the smallest integer $n\geq 4$ for which one can choose four different numbers $a,b,c$ and $d$ from any $n$ distinct integers such that $a+b-c-d$ is divisible by $20$.
Izvor: Međunarodna matematička olimpijada, shortlist 1998
Školjka 
for which one can choose four different numbers 
and 
from any 
distinct integers such that 
is divisible by 
.