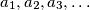
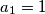
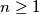
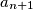
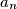
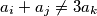
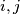
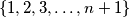
A sequence of integers is defined as follows: and for , is the smallest integer greater than such that for any and in , not necessarily distinct. Determine .
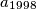
%V0
A sequence of integers $a_{1},a_{2},a_{3},\ldots$ is defined as follows: $a_{1} = 1$ and for $n\geq 1$, $a_{n + 1}$ is the smallest integer greater than $a_{n}$ such that $a_{i} + a_{j}\neq 3a_{k}$ for any $i,j$ and $k$ in $\{1,2,3,\ldots ,n + 1\}$, not necessarily distinct. Determine $a_{1998}$.
Izvor: Međunarodna matematička olimpijada, shortlist 1998
Školjka 
is defined as follows: 
and for 
, 
is the smallest integer greater than 
such that 
for any 
and 
in 
, not necessarily distinct. Determine 
.