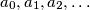
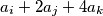
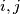
Let be an increasing sequence of nonnegative integers such that every nonnegative integer can be expressed uniquely in the form , where and are not necessarily distinct. Determine .
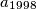
%V0
Let $a_{0},a_{1},a_{2},\ldots$ be an increasing sequence of nonnegative integers such that every nonnegative integer can be expressed uniquely in the form $a_{i}+2a_{j}+4a_{k}$, where $i,j$ and $k$ are not necessarily distinct. Determine $a_{1998}$.
Izvor: Međunarodna matematička olimpijada, shortlist 1998
Školjka 
be an increasing sequence of nonnegative integers such that every nonnegative integer can be expressed uniquely in the form 
, where 
and 
are not necessarily distinct. Determine 
.