IMO Shortlist 1999 problem A4
Dodao/la:
arhiva2. travnja 2012. Prove that the set of positive integers cannot be partitioned into three nonempty subsets such that, for any two integers
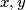
taken from two different subsets, the number
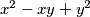
belongs to the third subset.
%V0
Prove that the set of positive integers cannot be partitioned into three nonempty subsets such that, for any two integers $x,y$ taken from two different subsets, the number $x^2-xy+y^2$ belongs to the third subset.
Izvor: Međunarodna matematička olimpijada, shortlist 1999