IMO Shortlist 1999 problem C2
Dodao/la:
arhiva2. travnja 2012. If a
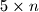
rectangle can be tiled using

pieces like those shown in the diagram, prove that

is even. Show that there are more than
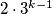
ways to file a fixed
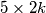
rectangle
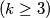
with
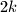
pieces. (symmetric constructions are supposed to be different.)
%V0
If a $5 \times n$ rectangle can be tiled using $n$ pieces like those shown in the diagram, prove that $n$ is even. Show that there are more than $2 \cdot 3^{k-1}$ ways to file a fixed $5 \times 2k$ rectangle $(k \geq 3)$ with $2k$ pieces. (symmetric constructions are supposed to be different.)
Izvor: Međunarodna matematička olimpijada, shortlist 1999