IMO Shortlist 1999 problem G7
Dodao/la:
arhiva2. travnja 2012. The point

is inside the convex quadrilateral

, such that
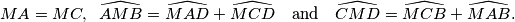
Prove that
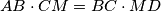
and
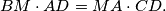
%V0
The point $M$ is inside the convex quadrilateral $ABCD$, such that $$MA = MC,\hspace{0,2cm}\widehat{AMB} = \widehat{MAD} + \widehat{MCD} \quad \textnormal{and} \quad \widehat{CMD} = \widehat{MCB} + \widehat{MAB}\text{.}$$
Prove that $AB \cdot CM = BC \cdot MD$ and $BM \cdot AD = MA \cdot CD.$
Izvor: Međunarodna matematička olimpijada, shortlist 1999