IMO Shortlist 1999 problem N4
Dodao/la:
arhiva2. travnja 2012. Denote by S the set of all primes such the decimal representation of
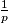
has the fundamental period divisible by 3. For every
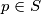
such that
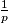
has the fundamental period
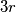
one may write
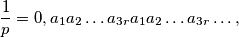
where
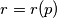
; for every
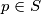
and every integer
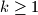
define
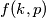
by
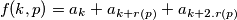
a) Prove that

is infinite.
b) Find the highest value of
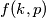
for
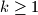
and
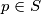
%V0
Denote by S the set of all primes such the decimal representation of $\frac{1}{p}$ has the fundamental period divisible by 3. For every $p \in S$ such that $\frac{1}{p}$ has the fundamental period $3r$ one may write
$$\frac{1}{p}=0,a_{1}a_{2}\ldots a_{3r}a_{1}a_{2} \ldots a_{3r} \ldots ,$$
where $r=r(p)$; for every $p \in S$ and every integer $k \geq 1$ define $f(k,p)$ by $$f(k,p)= a_{k}+a_{k+r(p)}+a_{k+2.r(p)}$$
a) Prove that $S$ is infinite.
b) Find the highest value of $f(k,p)$ for $k \geq 1$ and $p \in S$
Izvor: Međunarodna matematička olimpijada, shortlist 1999