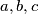
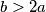
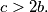
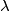
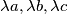
Let be positive integers satisfying the conditions and Show that there exists a real number with the property that all the three numbers have their fractional parts lying in the interval
%V0
Let $a, b, c$ be positive integers satisfying the conditions $b > 2a$ and $c > 2b.$ Show that there exists a real number $\lambda$ with the property that all the three numbers $\lambda a, \lambda b, \lambda c$ have their fractional parts lying in the interval $\left(\frac {1}{3}, \frac {2}{3} \right].$
Izvor: Međunarodna matematička olimpijada, shortlist 2000
Školjka 
be positive integers satisfying the conditions 
and 
Show that there exists a real number 
with the property that all the three numbers 
have their fractional parts lying in the interval ![\left(\frac {1}{3}, \frac {2}{3} \right].](/media/m/c/f/e/cfe91f93cf6950a9edc579467b2af1f5.png)