IMO Shortlist 2000 problem A4
Dodao/la:
arhiva2. travnja 2012. The function

is defined on the set of nonnegative integers and takes nonnegative integer values satisfying the following conditions: for every
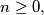
(i)
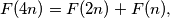
(ii)
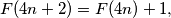
(iii)
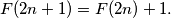
Prove that for each positive integer
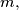
the number of integers

with
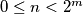
and
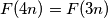
is
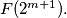
%V0
The function $F$ is defined on the set of nonnegative integers and takes nonnegative integer values satisfying the following conditions: for every $n \geq 0,$
(i) $F(4n) = F(2n) + F(n),$
(ii) $F(4n + 2) = F(4n) + 1,$
(iii) $F(2n + 1) = F(2n) + 1.$
Prove that for each positive integer $m,$ the number of integers $n$ with $0 \leq n < 2^m$ and $F(4n) = F(3n)$ is $F(2^{m + 1}).$
Izvor: Međunarodna matematička olimpijada, shortlist 2000