IMO Shortlist 2000 problem A6
Dodao/la:
arhiva2. travnja 2012. A nonempty set

of real numbers is called a
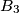
-set if the conditions
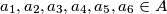
and
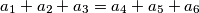
imply that the sequences
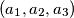
and
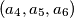
are identical up to a permutation. Let
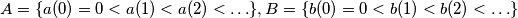
be infinite sequences of real numbers with
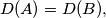
where, for a set

of real numbers,
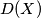
denotes the difference set
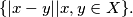
Prove that if

is a
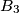
-set, then
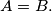
%V0
A nonempty set $A$ of real numbers is called a $B_3$-set if the conditions $a_1, a_2, a_3, a_4, a_5, a_6 \in A$ and $a_1 + a_2 + a_3 = a_4 + a_5 + a_6$ imply that the sequences $(a_1, a_2, a_3)$ and $(a_4, a_5, a_6)$ are identical up to a permutation. Let
$$A = \{a(0) = 0 < a(1) < a(2) < \ldots \}, B = \{b(0) = 0 < b(1) < b(2) < \ldots \}$$
be infinite sequences of real numbers with $D(A) = D(B),$ where, for a set $X$ of real numbers, $D(X)$ denotes the difference set $\{|x-y| | x, y \in X \}.$ Prove that if $A$ is a $B_3$-set, then $A = B.$
Izvor: Međunarodna matematička olimpijada, shortlist 2000