IMO Shortlist 2000 problem C3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Let 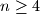 be a fixed positive integer. Given a set
be a fixed positive integer. Given a set 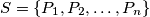 of
of  points in the plane such that no three are collinear and no four concyclic, let
points in the plane such that no three are collinear and no four concyclic, let 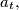
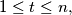 be the number of circles
be the number of circles 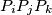 that contain
that contain 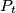 in their interior, and let
in their interior, and let 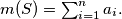 Prove that there exists a positive integer
Prove that there exists a positive integer 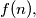 depending only on
depending only on 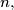 such that the points of
such that the points of  are the vertices of a convex polygon if and only if
are the vertices of a convex polygon if and only if 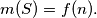
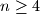 be a fixed positive integer. Given a set
be a fixed positive integer. Given a set 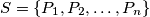 of
of  points in the plane such that no three are collinear and no four concyclic, let
points in the plane such that no three are collinear and no four concyclic, let 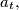
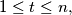 be the number of circles
be the number of circles 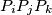 that contain
that contain 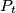 in their interior, and let
in their interior, and let 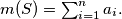 Prove that there exists a positive integer
Prove that there exists a positive integer 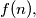 depending only on
depending only on 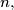 such that the points of
such that the points of  are the vertices of a convex polygon if and only if
are the vertices of a convex polygon if and only if 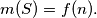
Izvor: Međunarodna matematička olimpijada, shortlist 2000
 Školjka
Školjka 
