IMO Shortlist 2000 problem C4
Dodao/la:
arhiva2. travnja 2012. Let

and

be positive integers such that
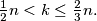
Find the least number

for which it is possible to place

pawns on

squares of an
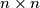
chessboard so that no column or row contains a block of

adjacent unoccupied squares.
%V0
Let $n$ and $k$ be positive integers such that $\frac{1}{2} n < k \leq \frac{2}{3} n.$ Find the least number $m$ for which it is possible to place $m$ pawns on $m$ squares of an $n \times n$ chessboard so that no column or row contains a block of $k$ adjacent unoccupied squares.
Izvor: Međunarodna matematička olimpijada, shortlist 2000