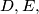
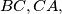
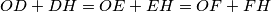
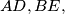
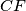
Let be the circumcenter and the orthocenter of an acute triangle Show that there exist points and on sides and respectively such that and the lines and are concurrent.
%V0
Let $O$ be the circumcenter and $H$ the orthocenter of an acute triangle $ABC.$ Show that there exist points $D, E,$ and $F$ on sides $BC,CA,$ and $AB$ respectively such that $$OD + DH = OE +EH = OF +FH$$ and the lines $AD, BE,$ and $CF$ are concurrent.
Izvor: Međunarodna matematička olimpijada, shortlist 2000
Školjka 
be the circumcenter and 
the orthocenter of an acute triangle 
Show that there exist points 
and 
on sides 
and 
respectively such that 
and the lines 
and 
are concurrent.