IMO Shortlist 2000 problem G6
Dodao/la:
arhiva2. travnja 2012. Let

be a convex quadrilateral. The perpendicular bisectors of its sides

and

meet at

. Denote by

a point inside the quadrilateral

such that
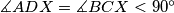
and
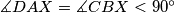
. Show that
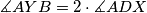
.
%V0
Let $ABCD$ be a convex quadrilateral. The perpendicular bisectors of its sides $AB$ and $CD$ meet at $Y$. Denote by $X$ a point inside the quadrilateral $ABCD$ such that $\measuredangle ADX = \measuredangle BCX < 90^{\circ}$ and $\measuredangle DAX = \measuredangle CBX < 90^{\circ}$. Show that $\measuredangle AYB = 2\cdot\measuredangle ADX$.
Izvor: Međunarodna matematička olimpijada, shortlist 2000