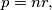
Prove that there exist infinitely many positive integers such that where and are respectively the semiperimeter and the inradius of a triangle with integer side lengths.
%V0
Prove that there exist infinitely many positive integers $n$ such that $p = nr,$ where $p$ and $r$ are respectively the semiperimeter and the inradius of a triangle with integer side lengths.
Izvor: Međunarodna matematička olimpijada, shortlist 2000
Školjka 
such that 
where 
and 
are respectively the semiperimeter and the inradius of a triangle with integer side lengths.