IMO Shortlist 2001 problem C1
Dodao/la:
arhiva2. travnja 2012. Let
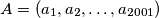
be a sequence of positive integers. Let

be the number of 3-element subsequences
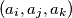
with
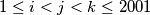
, such that
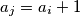
and
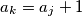
. Considering all such sequences

, find the greatest value of

.
%V0
Let $A = (a_1, a_2, \ldots, a_{2001})$ be a sequence of positive integers. Let $m$ be the number of 3-element subsequences $(a_i,a_j,a_k)$ with $1 \leq i < j < k \leq 2001$, such that $a_j = a_i + 1$ and $a_k = a_j + 1$. Considering all such sequences $A$, find the greatest value of $m$.
Izvor: Međunarodna matematička olimpijada, shortlist 2001