IMO Shortlist 2001 problem C6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 For a positive integer  define a sequence of zeros and ones to be balanced if it contains
define a sequence of zeros and ones to be balanced if it contains  zeros and
zeros and  ones. Two balanced sequences
ones. Two balanced sequences  and
and  are neighbors if you can move one of the
are neighbors if you can move one of the  symbols of
symbols of  to another position to form
to another position to form  . For instance, when
. For instance, when 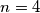 , the balanced sequences
, the balanced sequences 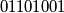 and
and 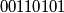 are neighbors because the third (or fourth) zero in the first sequence can be moved to the first or second position to form the second sequence. Prove that there is a set
are neighbors because the third (or fourth) zero in the first sequence can be moved to the first or second position to form the second sequence. Prove that there is a set  of at most
of at most 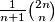 balanced sequences such that every balanced sequence is equal to or is a neighbor of at least one sequence in
balanced sequences such that every balanced sequence is equal to or is a neighbor of at least one sequence in  .
.
 define a sequence of zeros and ones to be balanced if it contains
define a sequence of zeros and ones to be balanced if it contains  zeros and
zeros and  ones. Two balanced sequences
ones. Two balanced sequences  and
and  are neighbors if you can move one of the
are neighbors if you can move one of the  symbols of
symbols of  to another position to form
to another position to form  . For instance, when
. For instance, when 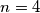 , the balanced sequences
, the balanced sequences 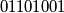 and
and 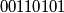 are neighbors because the third (or fourth) zero in the first sequence can be moved to the first or second position to form the second sequence. Prove that there is a set
are neighbors because the third (or fourth) zero in the first sequence can be moved to the first or second position to form the second sequence. Prove that there is a set  of at most
of at most 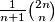 balanced sequences such that every balanced sequence is equal to or is a neighbor of at least one sequence in
balanced sequences such that every balanced sequence is equal to or is a neighbor of at least one sequence in  .
. Izvor: Međunarodna matematička olimpijada, shortlist 2001
 Školjka
Školjka 
