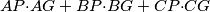
Let be a triangle with centroid . Determine, with proof, the position of the point in the plane of such that is a minimum, and express this minimum value in terms of the side lengths of .
%V0
Let $ABC$ be a triangle with centroid $G$. Determine, with proof, the position of the point $P$ in the plane of $ABC$ such that $AP{\cdot}AG + BP{\cdot}BG + CP{\cdot}CG$ is a minimum, and express this minimum value in terms of the side lengths of $ABC$.
Izvor: Međunarodna matematička olimpijada, shortlist 2001
Školjka 
be a triangle with centroid 
. Determine, with proof, the position of the point 
in the plane of 
is a minimum, and express this minimum value in terms of the side lengths of