IMO Shortlist 2001 problem G4
Dodao/la:
arhiva2. travnja 2012. Let

be a point in the interior of triangle

. Let
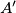
lie on

with
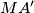
perpendicular to

. Define
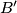
on

and
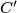
on

similarly. Define
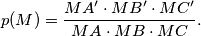
Determine, with proof, the location of

such that
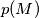
is maximal. Let
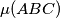
denote this maximum value. For which triangles

is the value of
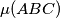
maximal?
%V0
Let $M$ be a point in the interior of triangle $ABC$. Let $A'$ lie on $BC$ with $MA'$ perpendicular to $BC$. Define $B'$ on $CA$ and $C'$ on $AB$ similarly. Define
$$p(M) = \frac{MA' \cdot MB' \cdot MC'}{MA \cdot MB \cdot MC}.$$
Determine, with proof, the location of $M$ such that $p(M)$ is maximal. Let $\mu(ABC)$ denote this maximum value. For which triangles $ABC$ is the value of $\mu(ABC)$ maximal?
Izvor: Međunarodna matematička olimpijada, shortlist 2001