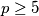
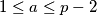
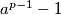
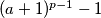
Let be a prime number. Prove that there exists an integer with such that neither nor is divisible by .
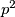
%V0
Let $p \geq 5$ be a prime number. Prove that there exists an integer $a$ with $1 \leq a \leq p-2$ such that neither $a^{p-1}-1$ nor $(a+1)^{p-1}-1$ is divisible by $p^2$.
Izvor: Međunarodna matematička olimpijada, shortlist 2001
Školjka 
be a prime number. Prove that there exists an integer 
with 
such that neither 
nor 
is divisible by 
.