IMO Shortlist 2002 problem A5
Dodao/la:
arhiva2. travnja 2012. Let

be a positive integer that is not a perfect cube. Define real numbers

by
![a=\root3\of n\kern1.5pt,\qquad b={1\over a-[a]}\kern1pt,\qquad c={1\over b-[b]}\kern1.5pt,](/media/m/8/2/d/82d50c7f89d4ecc16f6afad9981c6d07.png)
where
![[x]](/media/m/6/a/4/6a47dfb91475b9d5490dbb3a666604a3.png)
denotes the integer part of

. Prove that there are infinitely many such integers

with the property that there exist integers
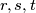
, not all zero, such that
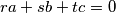
.
%V0
Let $n$ be a positive integer that is not a perfect cube. Define real numbers $a,b,c$ by
$$a=\root3\of n\kern1.5pt,\qquad b={1\over a-[a]}\kern1pt,\qquad c={1\over b-[b]}\kern1.5pt,$$
where $[x]$ denotes the integer part of $x$. Prove that there are infinitely many such integers $n$ with the property that there exist integers $r,s,t$, not all zero, such that $ra+sb+tc=0$.
Izvor: Međunarodna matematička olimpijada, shortlist 2002