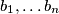
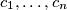
Let be a non-empty set of positive integers. Suppose that there are positive integers and such that
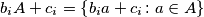
- for each the set is a subset of , and
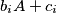
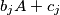
- the sets and are disjoint whenever
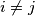
Prove that
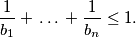
%V0
Let $A$ be a non-empty set of positive integers. Suppose that there are positive integers $b_1,\ldots b_n$ and $c_1,\ldots,c_n$ such that
- for each $i$ the set $b_iA+c_i=\left\{b_ia+c_i\colon a\in A\right\}$ is a subset of $A$, and
- the sets $b_iA+c_i$ and $b_jA+c_j$ are disjoint whenever $i\ne j$
Prove that $${1\over b_1}+\,\ldots\,+{1\over b_n}\leq1.$$
Source: Međunarodna matematička olimpijada, shortlist 2002
Školjka 
be a non-empty set of positive integers. Suppose that there are positive integers 
and 
such that 
the set 
is a subset of 
and 
are disjoint whenever 
