IMO Shortlist 2002 problem C4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Let  be the set of ordered triples
be the set of ordered triples 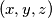 , where
, where 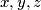 are integers with
are integers with 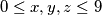 . Players
. Players  and
and  play the following guessing game. Player
play the following guessing game. Player  chooses a triple
chooses a triple 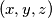 in
in  , and Player
, and Player  has to discover
has to discover  's triple in as few moves as possible. A move consists of the following:
's triple in as few moves as possible. A move consists of the following:  gives
gives  a triple
a triple 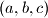 in
in  , and
, and  replies by giving
replies by giving  the number
the number 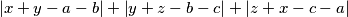 . Find the minimum number of moves that
. Find the minimum number of moves that  needs to be sure of determining
needs to be sure of determining  's triple.
's triple.
 be the set of ordered triples
be the set of ordered triples 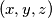 , where
, where 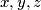 are integers with
are integers with 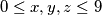 . Players
. Players  and
and  play the following guessing game. Player
play the following guessing game. Player  chooses a triple
chooses a triple 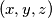 in
in  , and Player
, and Player  has to discover
has to discover  's triple in as few moves as possible. A move consists of the following:
's triple in as few moves as possible. A move consists of the following:  gives
gives  a triple
a triple 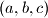 in
in  , and
, and  replies by giving
replies by giving  the number
the number 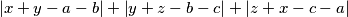 . Find the minimum number of moves that
. Find the minimum number of moves that  needs to be sure of determining
needs to be sure of determining  's triple.
's triple. Izvor: Međunarodna matematička olimpijada, shortlist 2002
 Školjka
Školjka 
