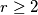
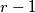
Let be a fixed positive integer, and let be an infinite family of sets, each of size , no two of which are disjoint. Prove that there exists a set of size that meets each set in .
%V0
Let $r\geq2$ be a fixed positive integer, and let $F$ be an infinite family of sets, each of size $r$, no two of which are disjoint. Prove that there exists a set of size $r-1$ that meets each set in $F$.
Izvor: Međunarodna matematička olimpijada, shortlist 2002
Školjka 
be a fixed positive integer, and let 
be an infinite family of sets, each of size 
, no two of which are disjoint. Prove that there exists a set of size 
that meets each set in