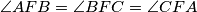
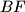
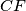
Let be a triangle for which there exists an interior point such that . Let the lines and meet the sides and at and respectively. Prove that
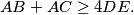
%V0
Let $ABC$ be a triangle for which there exists an interior point $F$ such that $\angle AFB=\angle BFC=\angle CFA$. Let the lines $BF$ and $CF$ meet the sides $AC$ and $AB$ at $D$ and $E$ respectively. Prove that
$$AB+AC\geq4DE.$$
Izvor: Međunarodna matematička olimpijada, shortlist 2002
Školjka 
be a triangle for which there exists an interior point 
such that 
. Let the lines 
and 
meet the sides 
and 
at 
and 
respectively. Prove that 