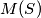
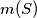
For any set of five points in the plane, no three of which are collinear, let and denote the greatest and smallest areas, respectively, of triangles determined by three points from . What is the minimum possible value of ?
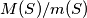
%V0
For any set $S$ of five points in the plane, no three of which are collinear, let $M(S)$ and $m(S)$ denote the greatest and smallest areas, respectively, of triangles determined by three points from $S$. What is the minimum possible value of $M(S)/m(S)$ ?
Izvor: Međunarodna matematička olimpijada, shortlist 2002
Školjka 
of five points in the plane, no three of which are collinear, let 
and 
denote the greatest and smallest areas, respectively, of triangles determined by three points from 
?