IMO Shortlist 2002 problem G8
Kvaliteta:
Avg: 4,0Težina:
Avg: 9,0 Let two circles 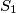 and
and 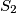 meet at the points
meet at the points  and
and  . A line through
. A line through  meets
meets 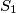 again at
again at  and
and 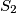 again at
again at  . Let
. Let  ,
,  ,
,  be three points on the line segments
be three points on the line segments  ,
,  ,
,  respectively, with
respectively, with  parallel to
parallel to  and
and 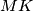 parallel to
parallel to  . Let
. Let  and
and  be points on those arcs
be points on those arcs  of
of 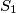 and
and  of
of 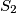 respectively that do not contain
respectively that do not contain  . Given that
. Given that 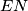 is perpendicular to
is perpendicular to  and
and 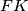 is perpendicular to
is perpendicular to  prove that
prove that 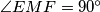 .
.
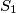 and
and 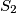 meet at the points
meet at the points  and
and  . A line through
. A line through  meets
meets 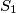 again at
again at  and
and 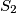 again at
again at  . Let
. Let  ,
,  ,
,  be three points on the line segments
be three points on the line segments  ,
,  ,
,  respectively, with
respectively, with  parallel to
parallel to  and
and 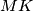 parallel to
parallel to  . Let
. Let  and
and  be points on those arcs
be points on those arcs  of
of 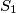 and
and  of
of 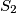 respectively that do not contain
respectively that do not contain  . Given that
. Given that 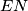 is perpendicular to
is perpendicular to  and
and 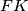 is perpendicular to
is perpendicular to  prove that
prove that 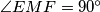 .
. Izvor: Međunarodna matematička olimpijada, shortlist 2002
 Školjka
Školjka 
